Entes geométricos fundamentales
Los entes geométricos fundamentales son aquellos que no admiten definición: por el contrario sí admiten una noción que nos sirve para contarle a otro de qué hablamos.
Ellas son: punto, recta y plano.
El punto se nombra con las letras mayúscula del abecedario y se representan cuando uno apoya el lápiz sobre una hoja de un cuaderno o la marca que deja una tiza en el pizarrón. Colocamos una cruz.
Punto
A B
. .
El PUNTO es una «figura geométrica» adimensional: no tiene longitud, área, volumen, ni otro ángulo dimensional. No es un objeto físico. Describe una posición en el espacio, determinada respecto de un sistema de coordenadas preestablecido.
A los puntos se les suele nombrar con una letra mayúscula: A, B, C, etc.
El concepto de punto, como ente geométrico, surge en la antigua concepción griega de la geometría, compilada en Alejandría por Euclides en su tratado Los Elementos, dando una definición de punto excluyente: «lo que no tiene ninguna parte». El punto, en la geometría clásica se basa en la idea de que era un concepto intuitivo, el ente geométrico «sin dimensiones», y sólo era necesario asumir la noción de punto.
SEGMENTO
Un segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos.
ó también
Segmento es la porción de recta limitada por dos puntos, llamados extremos.
Este es el Segmento AB
Tipos de segmentos
Segmento nulo: Un segmento es nulo cuando sus extremos coinciden.
Ejemplo: Un punto
Segmentos consecutivos
Dos segmentos son consecutivos cuando tienen un extremo en común.
 |  |
Según pertenezcan o no a la misma línea, se clasifican en:
Colineales
No colineales: Los segmentos consecutivos no colineales, llamados poligonal o quebrada, pueden ser abiertos o cerrados según tengan o no extremos comunes el primer y el último segmento que lo forman. Las poligonales cerradas forman polígonos.
La recta se nombra con las letras mayúsculas del abecedario que la determina, por lo menos dos puntos y es un conjunto infinito de puntos alineados.
En geometría euclidiana, la recta o línea recta, es el ente ideal que se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, o sea, no posee principio ni fin.
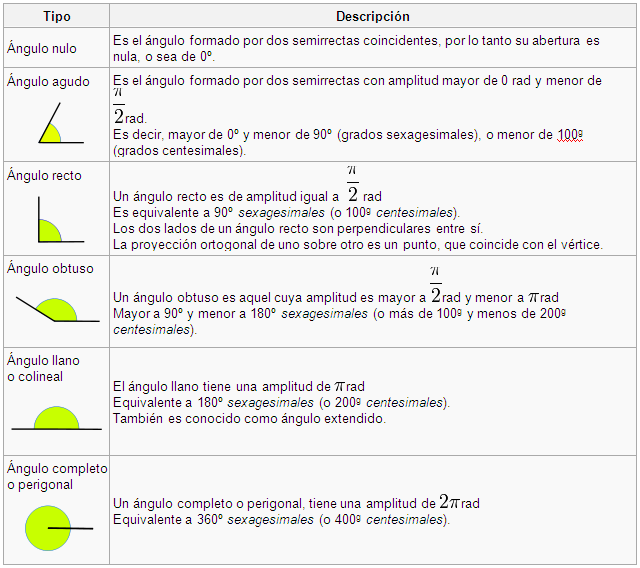
La Recta se nombra con una letra Minúscula o dos Mayúsculas y se lee la recta AB, la recta HG y la recta m.
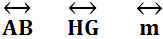
LA SEMIRECTA
La Semirecta se nombra con dos Mayúsculas y se lee la Semirecta AB, la Semirecta HG.
El plano se identifica con las letras minúsculas del alfabeto griego:se representa con una figura amorfa cerrada y es infinito.
En geometría, un plano es el ente ideal que sólo posee dos dimensiones y contiene infinitos puntos y rectas;es uno de los entes geométricos fundamentales junto con el punto y la recta.
los planos son especialmente utilizados en ingeniería, arquitectura y diseño ya que sirven para diagramar en una superficie plana otras superficies que son regularmente tridimensionales.
Un plano queda definido por los siguientes elementos geométricos:
- Tres puntos no alineados.
- Una recta y un punto exterior a ella.
- Dos rectas paralelas.
- Dos rectas que se cortan
En el plano dos rectas pueden tener las siguientes posiciones relativas:
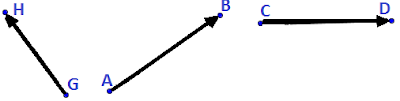
RECTAS SECANTES
(Rectas secantes son las que se cortan. Dos rectas secantes tienen un punto en común.)
Son las que situadas en un plano se cortan en un punto.
Las rectas A y B de la siguiente figura se cortan en el punto C. Estas rectas se dice también que son concurrentes o convergentes que significa que tienden a unirse o que la distancia entre ellas se va haciendo menor hasta cortarse en un punto
LÍNEAS CONVERGENTES
Son las que saliendo de dos puntos del mismo plano, a medida que avanzan se juntan en un punto dado:
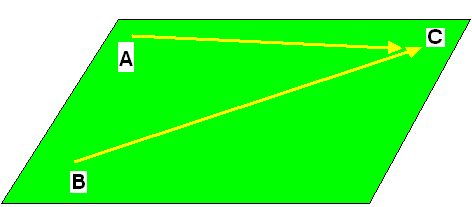
Como ves, las rectas han salido de los puntos A y B y si se prolongan, se juntarán en C.
LÍNEAS DIVERGENTES
Son las que saliendo del mismo punto, a medida que avanzan se van separando una de otra:
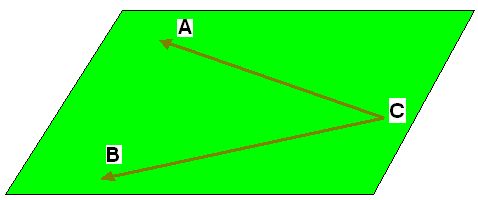
1-¿Dos rectas convergentes pueden llegar a cortarse?
2-Dos o más rectas secantes ¿podemos decir que son convergentes?
Rta: 1)sí,siempre que se las alarguen convenientemente.
2)sí, porque las rectas secantes se cortan se cortan
y por ello han de convergir, dirigirse a un punto.
RECTAS QUE SE CRUZAN
Las rectas que se cruzan están en distintos planos y por lo que no tienen ningún punto en común. Nunca se encuentran.
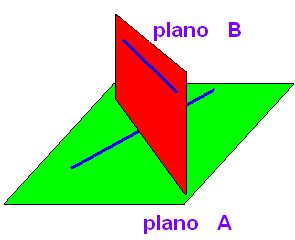
Las rectas que tienes a la izquierda en color azul están situadas en planos diferentes y comprobarás que no tienen, por mucho que se prolonguen, ningún punto en común
En la fotografía de la derecha puedes ver una autovía sobre una carretera y un río.
La autovía está en un plano superior a la carretera y el río.
También la carretera y el río están en planos diferentes.
También la carretera y el río están en planos diferentes.
Las líneas pintadas en blanco del centro de la carretera y de la autovía se cruzan.
Uno de los puentes más largos y más altos del mundo que se encuentra en el sur de Francia, se trata del Viaducto de Millau en Aveyron de 2460 metros de longitud, una anchura de 32 metros y una altura de 270 metros aunque desde el suelo hasta la parte alta de los postes hay 350 metros.
Puedes ver las distintas líneas que forman el río Tarn y muchas pequeñas carreteras, cada una en un plano distinto. Estas líneas y la calzada de la autovía de 6 carriles, se cruzan.
RECTAS PARALELAS Y PERPENDICULARES
1°) ¿Dos rectas paralelas se cortan siempre en un punto?
2°) ¿En cuántos puntos se cortan dos rectas paralelas?
3°) ¿Qué tienen en común dos rectas paralelas?
4°) ¿En cuántos puntos se cortan dos rectas perpendiculares?
5°) ¿Qué ángulo forman dos rectas perpendiculares que se cortan?
6°) ¿Cuánto mide el ángulo formado por la intersección de dos rectas perpendiculares?
7°) Si la recta T es paralela a S, y la recta R es perpendicular a S, ¿las rectas R y T son paralelas?
7°) Si la recta T es paralela a S, y la recta R es perpendicular a S, ¿las rectas R y T son paralelas?
8°) La distancia entre dos rectas paralelas es siempre la misma, ¿Es cierto?
9°) ¿Cómo se llaman a dos rectas que no se cortan en ningún punto?
10°) ¿Cómo se llaman a dos rectas que se cortan formando un ángulo recto?
NECESITAS AYUDA
NECESITAS AYUDA
Rectas Paralelas, perpendiculares y oblicuas(secantes)
en el plano( un par de ejes cartesianos)
Clasificación de los ángulos
Relaciones importantes entre dos ángulos
Ángulos consecutivos: Dos ángulos son consecutivos si tienen el mismo vértice y un lado en
común.
Ángulos complementarios: Dos ángulos son complementarios si suman 90°. Los ángulos complementarios no necesitan tener el mismo vértice; pero en caso de tenerlo y tener también un lado común, serán dos ángulos consecutivos que forman un ángulo recto.
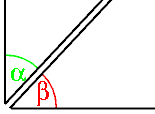
Ángulos suplementarios: Dos Ángulos son suplementarios si suman 180°
Los ángulos suplementarios no necesitan tener el mismo vértice. en caso de tenerlo, y tener también un lado común, serán dos ángulos consecutivos que forman un ángulo llano.
Ángulos adyascentes: Son dos ángulos consecutivos y suplementarios.
Ángulos Opuestos por el Vértice: Son los que tienen el mismo vértice y sus lados son semirrectas opuestas.
Propiedades: " Los ángulos opuestos por el vértice son iguales" ( técnicamente se dice . congruentes)
Los ángulos opuestos por el vértice ocurren siempre de a pares, un par son ángulos agudos y el otro par, son obtusos; o bien, los cuatro son ángulos rectos. Los ángulos de pares distintos ( uno agudo y otro obtuso) son adyascentes, y por lo tanto, suplementarios.
Medición de ángulos: Sistema sexagesimal
Profe. Susana
Relaciones entre los ángulos formados por dos rectas paralelas cortadas por una trasversal ( secante)
Si se intersecan dos rectas paralelas por una transversal ( recta secante), se obtienen 8 ( ocho) ángulos, 4 en cada punto de intersección. Se trata de nombrar y relacionar los pares de ángulos que podemos formar, uno tomado en un punto de intersección, con otro tomado en el otro punto de intersección. Así por ejemplo, en la figura siguiente, se relacionará uno de los ángulos del grupo 1, 2, 3, 4 con uno de los ángulos del grupo 5, 6, 7, 8
Ángulos correspondientes:
Ejercicio: Si el ángulo b mide 53°, encuentra los ángulos restantes
http://www.vitutor.net/1/clasificacion_angulos.html
8°)
a) El ángulo r mide 43°, encuentra la amplitud de los restantes.
b)
c)
9°) Calcule cada uno de los ángulos suplementarios
10°) Observa el gráfico y nombra:
a) El suplemento del ángulo m
b) El suplemento del ángulo (n+p)
c) El complemento del ángulo p
d) El complemento del ángulo m
DATOS:
el ángulo m= 57°
ángulo p= 46°
11) Dados los ángulos m y n cuyas amplitudes son respectivamente. de 38 grados,15 min y17 grados, 38 min. calculen sus amplitudes:
a) el complemento de la diferencia entre m y n
b) el suplemento de la suma entre m y n
c) la mitad del complemento de p
d) el triple de (m-n)
e) la tercera parte del suplemento de m
Práctico
1°) Menciona 5 objetos cuyas forma sugiera un punto en alguna de sus partes.
2°) Menciona tres objetos o situaciones que ilustren la idea de rectas o de una parte de ella.
3°) Menciona 5 objetos cuyas formas sugieren un plano en alguna de sus partes.
4°) Menciona 3 objetos, como el globo, que sugieran la idea de espacio.
5°) Dibuja tres puntos que sean colineales.
6°) En un grupo de 7 puntos , dibuja una recta a través de grupos de 3 o más puntos colineales.
7°) Calcula la amplitud de los tres ángulos restantes y justifica
a)
b)El ángulo obtuso mide156°.Encuentra
los ángulos restantes. Coloca los nombres faltantes.
7°) Calcula la amplitud de los tres ángulos restantes y justifica
a)
b)El ángulo obtuso mide156°.Encuentra
8°)
b)
9°) Calcule cada uno de los ángulos suplementarios
10°) Observa el gráfico y nombra:
a) El suplemento del ángulo m
b) El suplemento del ángulo (n+p)
c) El complemento del ángulo p
d) El complemento del ángulo m
DATOS:
el ángulo m= 57°
ángulo p= 46°
a) el complemento de la diferencia entre m y n
b) el suplemento de la suma entre m y n
c) la mitad del complemento de p
d) el triple de (m-n)
e) la tercera parte del suplemento de m
